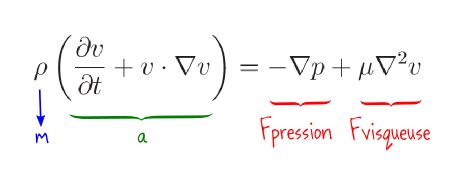L'équation de Navier-Stokes est l'une des plus importantes de toute la physique. Si elle n'a pas la chance d'être aussi connue que E=mc2, elle nous sert pourtant à prédire la météo, simuler les océans, optimiser les ailes des avions et même améliorer le réalisme des jeux vidéos.

Bien qu'elle fut établie au XIXème siècle, elle continue de fasciner les ingénieurs, les physiciens et même les mathématiciens. Il faut dire qu'on a promis 1 million de dollars à celui qui percerait les mystères de l'équation de Navier-Stokes. Un exploit récemment revendiqué par un mathématicien kazakh, et dont on verra ce qu'il faut en penser.

Comment décrire le mouvement des fluides ?

Puisque ce billet parle de l'équation de Navier-Stokes, je vais évidemment vous l'écrire. Mais ça n'est pas là le plus important ! Elle peut paraître un peu cryptique et je voudrais surtout vous faire comprendre d'où elle vient et à quoi elle sert.

Le principal objectif de cette équation, c'est de décrire le mouvement des fluides. Puisqu'un fluide, ça peut être un liquide ou un gaz, on comprend que l'équation de Navier-Stokes concerne tout un tas de choses qui nous entourent. On peut l'utiliser par exemple pour comprendre les mouvements des courants dans les océans, ainsi que ceux des grandes masses d'air dans l'atmosphère. On s'en sert également pour étudier la circulation du sang dans nos artères, et simuler la trajectoire de l'air autour d'une aile d'avion ou d'une carrosserie de voiture. Cette équation est même utilisée dans les jeux vidéos pour améliorer le réalisme de certaines scènes [1]. L'équation de Navier-Stokes est donc un must pour les ingénieurs de tous domaines.

Pour décrire correctement un fluide en mouvement, il faut connaître sa vitesse en tout point de l'espace. C'est ce qu'on appelle son champ de vitesse. L'image ci-dessous montre un exemple de champ de vitesse dans un fluide autour d'une aile d'avion, champ que l'on représente traditionnellement avec des petites flèches plus ou moins longues, proportionnelles à la vitesse et orientées dans le sens de l'écoulement (ici dans le référentiel du sol)

champ vitesse

L'équation de Navier-Stokes, établie au XIXème siècle par le français Navier et le britannique Stokes, c'est une équation qui permet de décrire le champ de vitesse d'un fluide. Plus précisément, il s'agit d'une équation différentielle dont le champ de vitesse est l'inconnue.

A quoi ressemble l'équation ?

Pour les non-initiés, la forme de l'équation est un peu rebutante, mais l'important est de comprendre en gros ce qu'elle représente. En mécanique, quand on étudie le mouvement des skieurs, des ressorts ou des boulets de canons, on écrit la loi de Newton « Somme des forces = ma » où m est la masse et a l'accélération. L'équation de Navier-Stokes ne dit pas autre chose que « Somme des forces = ma », mais comme on parle du champ de vitesse d'un fluide, la forme est un peu plus compliquée que pour un boulet de canon.

Dans un fluide, on va considérer deux types de forces : les forces de pression et les forces visqueuses. Les forces de pression, ce sont celles qui viennent du fait qu'un petit morceau du fluide se fait pousser par tout le reste du fluide qui l'entoure. Les forces visqueuses, ce sont l'équivalent des forces de frottement pour un skieur. Quand un morceau de fluide glisse sur un autre, il y a un frottement qui le freine et qui est d'autant plus important que le fluide est visqueux. Dans l'équation, on verra donc apparaître un paramètre μ qui représente la viscosité du fluide.

Voici donc l'équation de Navier-Stokes, et en quoi elle est l'analogue de « Somme des forces = m a » pour un fluide :

Equation navier stokes

Ici v est le champ de vitesse, p est la pression, ρ la masse volumique du fluide et μ sa viscosité. Encore une fois, vous n'êtes pas obligés de piger les détails de l'équation, mais nous allons considérer globalement ses propriétés, et voir ce qu'on peut en dire.

[Petite remarque pour ceux qui connaissent les EDP : la pression est aussi une inconnue de l'équation. Comme le champ de vitesse a 3 composantes, cela fait 4 inconnues pour 3 équations. Il manque donc une équation ! Si on suppose le fluide incompressible, il faut ajouter une condition qui est que le champ de vitesse est de divergence nulle - ce qui traduit aussi la conservation de la masse]

Pourquoi l'équation est-elle si compliquée ?

Il y a deux manières de comprendre pourquoi l'équation de Navier-Stokes est compliquée : la vision mathématique et la vision physique. Pour le mathématicien, l'équation est compliquée parce que c'est une équation différentielle non-linéaire. Si vous la comparez à l'équation qui décrit le mouvement d'un ressort (ou même, pour ceux qui connaissent, à l'équation de Maxwell ou à celle de la chaleur), la complication vient du terme v⋅∇v. Ce terme varie comme le carré du champ de vitesse, et c'est lui qui rend l'équation mathématiquement inextricable. En maths, la non-linéarité complique les choses, mais en physique aussi ! Car ce terme non-linéaire a sa traduction dans la complexité des phénomènes physiques décrits. Voyons en quoi.

avion turbulenceJe vous l'ai dit, l'équation de Navier-Stokes sert à décrire le mouvement des fluides. Ça veut dire qu'elle s'applique aussi bien au mouvement de l'huile d'olive versée d'une bouteille, qu'à celui de l'air au passage d'un avion. Or vous pouvez facilement imaginer que les deux situations n'ont rien à voir !

Dans le cas de la bouteille d'huile, le mouvement du fluide est tout ce qu'il y a de plus tranquille et régulier. Dans le cas de l'air au passage de l'avion, c'est le chaos total. C'est ce que montre l'image ci-contre, qui permet de visualiser à l'aide de fumée colorée le genre de mouvements de l'air qui se produit au décollage d'un petit avion.

Ce comportement chaotique, c'est ce qu'on appelle la turbulence. Et cette turbulence est le pendant physique de la non-linéarité de l'équation de Navier-Stokes.

Il existe de nombreuses anecdotes au sujet du problème de la turbulence. Léonard de Vinci avait déjà été intrigué par le problème, comme en témoignent ses magnifiques croquis que l'on voit ci-contre. Le physicien Richard Feynman considérait qu'il s'agissait du plus grand problème de la physique classique, quant au mathématicien Horace Lamb, il aurait affirmé que ce serait la première question qu'il poserait à Dieu en arrivant au paradis.

Comme nous l'avons dit, dans certaines situations (l'huile dans la bouteille), l'écoulement des fluides se fait de manière tranquille. C'est ce qu'on appelle le régime « laminaire ». Il se produit quand les fluides sont visqueux, lents et plutôt confinés.

A l'opposé, quand les fluides sont peu visqueux, rapides et se déplacent sur de grandes distances, les écoulements se produisent de manière chaotique et présentent de nombreux tourbillons : c'est ce qu'on appelle le régime turbulent. La transition entre les deux peut être assez soudaine (voir mon billet sur le nombre de Reynolds) et expérimentalement, pour un écoulement donné, on sait assez bien dire si l'on sera laminaire ou turbulent.

Mais mathématiquement, on n'en a aucune idée ! On aurait très envie d'être capables de démontrer rigoureusement que pour certaines valeurs de vitesse ou de viscosité, les solutions de l'équation de Navier-Stokes seront turbulentes, et pour d'autres elles seront laminaires. Mais personne ne sait établir ce lien explicitement. Pour traiter la turbulence, les physiciens en sont donc réduits à oublier l'équation de Navier-Stokes et à envisager le problème de manière statistique. Comprendre la physique de la turbulence est un sujet de recherche extrêmement actif aujourd'hui ! Mais revenons un peu aux maths...

Un prix à 1 million de dollars

Vous connaissez peut-être l'histoire, la fondation Clay a décidé en l'an 2000 de choisir 7 problèmes mathématiques « du millénaire », et de promettre 1 million de dollar à quiconque en résoudrait un. L'un de ces problèmes (la conjecture de Poincaré) a déjà été résolu par un mathématicien russe Grigori Perelman (qui a d'ailleurs refusé de toucher le prix et même de recevoir la médaille Fields; voilà qui ne va pas améliorer l'image des matheux, heureusement qu'on a Cédric Villani).

Pour comprendre sur quoi porte le problème à 100 patates de l'équation de Navier-Stokes, considérons le cas plus simple de l'équation qui régit le mouvement d'une masse m au bout d'un ressort de raideur k. Si on écrit toujours « Somme des forces = ma », on obtient l'équation différentielle suivante sur la position de la masse

md2xdt2=−kx

Il s'agit d'une équation différentielle du second ordre dont l'inconnue est x(t). Pour la résoudre, il faut spécifier les conditions initiales que sont la position x(0) et la vitesse dx/dt(0). Si ces conditions initiales sont données, on peut montrer qu'il existe une unique solution à l'équation, que cette solution est bien définie pour tout temps t allant de 0 à l'infini. On peut même calculer explicitement cette solution (programme de Terminale S j'imagine).

Dans le cas de Navier-Stokes, on n'est sûrs de rien ! Trouver une solution explicite est certainement totalement inaccessible. Mais même sans cela, si on se donne une condition initiale - c'est-à-dire le champ de vitesse à l'instant initial v(0) - on ne sait même pas montrer qu'il existe bien une unique solution bien définie pour tout temps t ! Vous vous rendez compte, cette équation est utilisée tous les jours par des ingénieurs pour calculer des trucs, et on ne sait même pas montrer qu'elle a effectivement des solutions !

Alors si vous voulez aider, et que vous ambitionnez de réclamer le million de dollars, il vous faudra faire l'une des deux choses suivantes :

    Démontrer que pour toute condition initiale, il existe une solution régulière et globalement définie (c'est-à-dire définie pour tout t de 0 à l'infini)
    OU Trouver un contre-exemple, c'est-à-dire une condition initiale v(0) telle que vous démontriez qu'il n'existe PAS de solution régulière globalement définie.

Où en est-on dans le problème ?

Quand le problème a été posé par la fondation Clay, on savait déjà plusieurs choses au sujet de l'équation. D'une part, en deux dimensions, on sait démontrer qu'il existe toujours une solution. C'est bien, mais le problème en 2D est beaucoup moins compliqué qu'en 3D. On sait également que si le champ de vitesse initial est suffisamment petit, il existe toujours une solution régulière globalement définie. Physiquement, cela correspond aux régimes où on est sûrs que l'écoulement sera laminaire et pas turbulent, et donc on évite l'influence forte des non-linéarités.

Plus subtil, on sait démontrer que pour toute condition initiale il existe une solution, et que cette solution est définie au moins pendant une durée finie [0;T], où la valeur de T dépend de la condition initiale. Ce qu'il « reste » à faire pour toucher les patates, c'est de montrer qu'une solution est toujours définie au-delà de T et ce jusqu'à l'infini.

Si vous voulez vous attaquer à la question, je vous recommande les quelques billets du génial Terry Tao sur le sujet, il y détaille notamment les types de stratégies envisageables. Il existe notamment une stratégie analogue à ce que qu'a fait Grigori Perelman pour la conjecture de Poincaré. Certains pensent aujourd'hui que ce dernier travaillerait d'ailleurs sur les équations de Navier-Stokes, histoire d'ajouter un second problème à 1 million à son tableau de chasse.

Pour finir, venons-en à la question de Mukhtarbay Otelbaev. Il s'agit de ce mathématicien kazakh prétendant avoir résolu le problème, et déclenchant ainsi pas mal de commentaires dans la presse (notamment la presse kazakhe) à la gloire du Kazakhstan, qui ne serait ainsi pas seulement la patrie de Borat.

L'article d'Otelbaev fait 100 pages et est écrit en russe [2]. Bon j'avoue même en français je n'y aurai rien compris. Mais Terry Tao a publié il y a quelques jours un article [3] qui semble mettre fin aux espoirs kazakhs. Si j'ai bien compris, il ne cite jamais explicitement Otelbaev, mais il démontre que son approche ne peut pas fonctionner.

Alors, Otelbaev, Perelman ou Tao. L'un des 3 parviendra-t-il à faire tomber le problème ? Affaire à suivre !

https://www.youtube.com/watch?v=nRSWIndKiiA

https://www.youtube.com/watch?v=v4zPW40vhHI