2.4 Conjecture sur l'altitude maximale de la montgolfière.

Au détour de nos réflexions, nous nous sommes dit : " Mais, finalement jusqu'où peut monter la montgolfière ? ". Pour répondre à cette question, nous restons dans le cas de la montgolfière définie précédemment et nous cherchons à connaître l'évolution des forces en fonction de l'altitude.

a°) Calcul de la poussée d'Archimède Пa en fonction de l'altitude :

Pour pouvoir calculer la poussée d'Archimède Пa en fonction de l'altitude, il est nécessaire de connaître la masse volumique de l'air en fonction de l'altitude, c'est-à-dire en fonction de la température et de la pression.

Dans un premier temps, nous avons donc cherché à connaître le lien entre température et altitude. Pour calculer cela , nous avons choisi la valeur du gradient thermique tel qu'il soit de -9.76°C/km soit -0.976°C/100m. Ce choix représente en fait l'évolution théorique de la température au regard du seul changement de pression : cette valeur a été choisie face à la nécessité de fixer une valeur la plus vraie possible pour la suite des calculs. Remarque: nous arrêterons nos calculs à 11000 m car au-delà de cette altitude moyenne, nous quittons la troposphère et le calcul précédent n'est plus admettable.

Par la suite, il est nécessaire de calculer la variation de la pression avec l'altitude. Il était nécessaire de trouver une formule reliant pression et altitude qui ne fasse pas intervenir la masse volumique de l'air. Nous prendrons donc la formule internationale du nivellement barométrique définie avec les valeurs fixées par l'O.A.C.I (Organisation de l'Aviation Civile Internationale).

Grâce à cette formule les valeurs de la pression ont été calculées (voir Annexe 2).

Puis, à l'aide de la loi des gaz parfaits [ P.V=n.R.θ --> Vm= (R.θ) / P] , nous avons calculé la masse volumique de l'air μair1.

Pour finir, nous avons pu calculer les valeurs de la poussée d'Archimède en fonction de la température (cf Annexe 2.a).

b°) Calcul du poids en fonction de la température et de la pression.

Pour calculer le poids, il faut connaître la variation de la masse volumique de l'air chauffé à une température constante fixée à 90°C.

Pour cela, il faut procéder au calcul de la masse volumique en fonction de l'altitude avec la température T = 90.0°C à l'aide de la loi des gaz parfaits. Etant donné que pour utiliser la loi des gaz parfaits, il faut connaître la variation de la pression en fonction de l'altitude, nous appliquerons la formule internationale du nivellement barométrique définie précédemment.

Pour finir, nous avons pu calculer les valeurs du poids en fonction de l'altitude (cf Annexe 2.b).

c°) Résultats et interprétation.

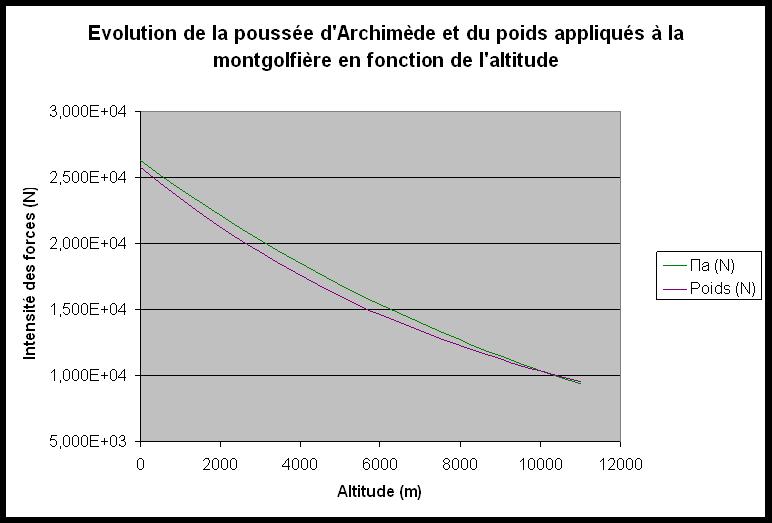
On remarque qu'entre 10000 et 11000 m, le poids devient supérieur à la poussée d'Archimède : la montgolfière redescend. Cependant, il faut remarquer que ces valeurs sont bien trop importantes pour être atteintes : le calcul théorique est possible mais dans les faits ce n'est pas réalisable. En effet, les hommes ne pourraient pas monter à cette altitude dans une simple nacelle, il faudrait une nacelle pressurisée. De plus, on remarque que la différence entre la température fixée de l'air du ballon (T=90°C) et la température extérieure (Text= -82,60 °C à 10'000 m) est trop importante : l'énergie fournie par les brûleurs devrait être énorme pour réussir à maintenir la température de l'air du ballon à 90°C.

Conclusion, même si mathématiquement le calcul est possible, la descente de la montgolfière n'est pas assurée par les forces physiques mais par l'action du pilote sur la montgolfière.